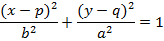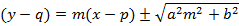Ellips Kurva Berderajat Dua

A. Pengertian Ellips

Ellips adalah himpunan semua titik yang jumlah jaraknya terhadap dua titik tertentu yang bukan elemen himpunan tersebut (titik fokus) selalu tetap. Dua titik fokus tersebut dilambangkan oleh F1dan F2. Ellips memiliki nilai esentrisitas kurang dari 1. Nilai esentrisitas adalah jarak suatu titik A ke titik fokus berbanding jarak titik A ke garis direktris. Makin besar nilai esentrisitas ellips, maka bentuk ellips akan semakin memanjang. Sebaliknya, makin kecil nilai esentrisitas ellips, maka bentuk ellips akan semakin membulat mendekati lingkaran.

B. Unsur-unsur Ellips
Unsur-unsur yang terdapat pada ellips dapat dilihat pada gambar berikut :

    Titik Pusat P (p, q)
    Titik Fokus: F1 dan F2
    Titik Puncak, titik puncak berada di sumbu mayor dan sumbu minor ellips
    Sumbu Mayor, yaitu sumbu simetris ellips yang paling panjang
    Sumbu Minor, yaitu sumbu simetris ellips yang paling pendek
    Garis Direktris, terdapat dua garis direktris pada ellips

  jarak titik fokus ke titik pusat dilambangkan dengan c

  jarak titik pusat ke titik puncak pada sumbu mayor dilambangkan dengan a
  jarak titik pusat ke titik puncak pada sumbu minor dilambangkan dengan b

C. Persamaan Ellips
1. Persamaan ellips yang berpusat di O (0, 0) dan titik fokus terletak pada sumbu x

2. Persamaan ellips yang berpusat di O (0, 0) dan titik fokus terletak pada sumbu y

3. Persamaan ellips yang berpusat di P (p, q) dan titik fokus terletak pada sumbu x

 
4. Persamaan ellips yang berpusat di P (p, q) dan titik fokus terletak pada sumbu y

 D. Latihan Soal

Tentukan persamaan ellips di bawah ini jika diketahui informasi berikut  :
1. titik fokus (0, -1) dan (8, -1), titik puncak (9, -1)
2. titik fokus (0, 2) dan ( 0, 6), titik puncak ((0, 0), (0, 8))

E. Persamaan Garis Singgung Ellips

    1. Persamaan Garis Singgung pada Ellips yang Berpusat di O (0, 0) :
       a. dengan garis bergradien m (y = mx + a)

       b. dengan titik singgung  T (x1, y1)

 

  2. Persamaan Garis Singgung pada Ellips yang Berpusat di P (p, q) :
      a.  dengan garis bergradien m (y = mx + a)

      b. dengan titik singgung  T (x1, y1)

Eksplorasi Soal-Soal Persamaan Bidang Datar dengan Pemecahan Masalah Polya

1.      Investigasi persamaan bidang yang melalui suatu titik dan tegak lurus pada vektor normal

1.      Understanding The Problem

a.       Tentukan apa saja yang akan ditemukan/dicari/diselesaikan!

Menentukan persamaan bidang yang melalui suatu titik dan tegak lurus pada vektor normal

b.      Informasi apa saja yang kamu peroleh dari permasalahan itu?

Titik P(1,2,3) dan vektor n= 2i-4j+k

2.      Devising a Plan

Strategi yang dipilih untuk menyelesaikan masalah ini yaitu :

a.       Membuat gambar di geogebra

1.      Input titik A(1,2,3) di kotak input

2.      Input vektor n = (2, -4, 1) di kotak input

3.      Input titik B(2, -4, 1) di kotak input

4.      Buat garis f yang melalui titik B dan C dengan menggunakan line

5.      Buat garis g tegak lurus terhadap garis f yang melalui titik A

6.      Buat bidang dengan menggunakan perpendicular plane yang melalui garis f dan g

3.      Carrying Out The Plan

Tahap ketiga pemecahan masalah yaitu menggunakan strategi untuk memecahkan masalah:

a.       Membuat gambar

KESIMPULAN :

Jadi, berdasarkan langkah pengerjaan diatas didapatkan persamaan bidang yang melalui titik P(1,2,3) dan tegak lurus vektor n=2i-4j+k adalah 2x-4y+z= -3.

4.      Looking Back

Langkah terakhir pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya.

r₀ = (x_0, y_0, z_{0) =} (1,2,3)

n= (a,b,c)= (2, -4, 1)

Persamaan bidang =

                                        =

                                                                =

₌

2.      Investigasi persamaan bidang yang melalui titik P(-4, -1, 2)  dan sejajar

a.      Bidang xy

b.      Bidang 2x-3y-4z=0

c.       Bidang 2x+4y-z=0

1.      Understanding The Problem

a.       Tentukan apa saja yang akan ditemukan/dicari/diselesaikan!

Menentukan persamaan bidang yang melalui suatu titik P(-4, -1, 2)  dan sejajar

b.      Informasi apa saja yang kamu peroleh dari permasalahan itu?

Titik P(-4, -1, 2)

2.      Devising a Plan

Strategi yang dipilih untuk menyelesaikan masalah ini yaitu :

a.       Membuat gambar di geogebra

·         Gambar a

1.      Input titik P(-4, -1, 2) di kotak input

2.      Buat bidang dengan menggunakan parallel plane yang melalui titik P dan sejajar dengan bidang xy

·         Gambar b

1.      Input titik P(-4, -1, 2) di kotak input

2.      Input persamaan bidang 2x-3y-4z=0 di kotak input

3.      Buat bidang dengan menggunakan parallel plane yang melalui titik P dan sejajar dengan bidang 2x-3y-4z=0

·         Gambar c

1.      Input titik P(-4, -1, 2) di kotak input

2.      Input persamaan bidang 2x + 4y - z = 6 di kotak input

3.      Buat bidang dengan menggunakan parallel plane yang melalui titik P dan sejajar dengan bidang 2x + 4y - z = 6

3.      Carrying Out The Plan

Tahap ketiga pemecahan masalah yaitu menggunakan strategi untuk memecahkan masalah:

a.       Membuat gambar

·         Gambar a

·         Gambar b

·         Gambar c

KESIMPULAN :

Jadi, berdasarkan langkah pengerjaan diatas didapatkan persamaan bidang yaitu

a.       Melalui titik P(-4,-1,2) dan sejajar bidang xy

Persamaan bidangnya adalah z = 2

b.      Melalui titik P(-4,-1,2) dan sejajar bidang 2x – 3y – 4z = 0

Persamaan bidangnya adalah   2x – 3y – 4z = -13

c.       Melalui titik P(-4,-1,2) dan sejajar bidang 2x + 4y – z = 6

Persamaan bidangnya adalah    2x + 4y – z = -14

4.      Looking Back

Langkah  terakhir  pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya.

a.       Melalui titik P(-4,-1,2) dan sejajar bidang xy

Karena sejajar bidang xy dan memaluli titik P(-4,-1,2) maka persamaan bidangnya adalaha z = 2

b.      Melalui titik P(-4,-1,2) dan sejajar bidang 2x – 3y – 4z = 0

Persamaan bidang   =  a    = 0

                                 = < 2, -3, -4 > <  x+4, y+1, z-2 > = 0

                                 = 2 (x+4) – 3( y+1) – 4(z-2) = 0

                                 = 2x + 8 – 3y- 3 – 4z +8 = 0

                                 = 2x – 3y – 4z = -13

Jadi persamaan bidangnya adalah 2x – 3y – 4z = -13

c.       Melalui titik P(-4,-1,2) dan sejajar bidang 2x + 4y – z = 6

Persamaan bidang   =  a    = 0

                                 = < 2, 4, -1 > <  x+4, y+1, z -2 > = 0

                                 = 2 (x+4) + 4( y+1) – 1(z-2) = 0

                                 = 2x + 8 + 4y + 4 – z +2 = 0

                                 = 2x + 4y – z = -14

Jadi persamaan bidangnya adalah 2x + 4y – z = -14

PERSAMAAN BOLA

Persamaan Bola

A.    Definisi Bola

Suatu bola, tepatnya (Permukaan Bola) merupakan tempat kedudukan titik ujung vektor-vektor di dalam ruang yang titik awalnya adalah titik tertentu, dan panjangnya adalah konstant.

Titik awal tertentu itu disebut TITIK PUSAT Bola, dan panjang vektor yang konstant itu disebut JARI-JARI Bola.

B.    Persamaan Bola

Persamaan Bola dengan pusat O(0 , 0, 0) dan jari-jari r adalah;

      

       x² + y² + z² = r² ....(I)

Persamaan Bola untuk Pusat Bola adalah M(a,b,c) dan jari-jari = R (lihat gambar berikut)

Ambil titik sebarang P(x˳, y˳, z˳) pada bola, maka berlaku:

MP = OP – OM

= (x˳, y˳, z˳) – (a, b, c)

= (x˳ – a. y˳ – b, z˳ – c)

Sehingga panjang vektor MP adalah │MP│, dimana:

│MP│ = √{ (x˳ – a)² + (y˳ – b)² + (z˳ – c)²}

Karena │MP│= R (jari-jari bola), maka:

R   = √{ (x˳ – a)² + (y˳ – b)² + (z˳ – c)²}

R² = (x˳ – a)² + (y˳ – b)² + (z˳ – c)²

Bila titik  P(x˳, y˳, z˳) dijalankan, maka diperoleh TK titik-titik yang dicari, yaitu persamaan Bola. Jadi persamaan Bola  yang berpusat dititik M(a,b,c) dengan jari-jari = R adalah......

                          (x – a)² + (y – b)² + (z – c)² = R² ….(II)

Bila persamaan (II) dijabarkan, maka akan diperoleh:

  (x – a)² + (y – b)² + (z – c)² = R²

  ( X² - 2ax + a²) + ( y² – 2by + b²) + (z² – 2cz + c²) = R²

    X² - 2ax + a² +  y² – 2by + b² + z² – 2cz + c²  = R²

   x² + y² + z² – 2ax – 2by – 2cz + a² + b² + c² – R² = 0

       x² + y² + z² – 2ax – 2by – 2cz + a² + b² + c² – R² = 0 … (III)

Dari persamaan (III) diatas, apabila:

• -2a = A
• -2b = B
• -2c = C dan 
•  a² + b² + c² – R² = D

 Maka dari persamaan (III) dapat ditulis sebagai berikut:

x² + y² + z² + Ax + By + Cz + D  = 0 ….(IV)

Persamaan (IV) ini  disebut  BENTUK UMUM persamaan Bola , dan karena:

•  -2a = A, maka a = -½ A
• -2b = B, maka b = -½B
•   -2c = C, maka c = -½C

Dengan demikian Pusat Bola pada persamaan (IV) diatas adalah...

M(-½A, -½B, -½C) ….(V)

Jadi, bentuk (V) diatas  adalah Rumus koordinat Titik Pusat Bola

Begitu pula karena  a² + b² + c² – R² = D, maka diperoleh :

R² =  a² + b² + c² – D

R² = (-½A)² + (-½B)² + (-½C)² – D

R² = ¼A² + ¼B² + ¼C² – D

         R² = √(¼A² + ¼B² + ¼C² – D) ….(VI)

Bentuk atau persamaan (VI) diatas adalah persamaan untuk JARI-JARI Bola

Untuk bola dengan persamaan  x² + y² + z² + Ax + By + Cz + D  = 0 (IV) diatas  terdapat tiga kemungkinan, yaitu :

1. Bila R² > 0, maka B adalah bola sejati

2. Bila R² = 0, maka B adalah bola titik (jari-jari = 0)

3. Bila R² < 0, maka B merupakan bola khayal  

C. Contoh soal dan pembahasannya

   1. Persamaan bola yang berpusat di (0,0,3) dan berjari-jari 5 adalah…..

Pembahasan :

(x-a)² + (y-b)² + (z-c)² = r²

(x-0)² + (y-0)² + (z-3)² = 5²

x² + y² + z² - 6z +9 = 25

x² + y² + z² - 6z = 25 - 9

x² + y² + z² - 6z = 16

     2. itik pusat dan jari-jari dari bola dengan persamaan 3x² + 3y² + 3z²- 6x + 12y – 18z -6 = 0

Pembahasan :

3x² + 3y² + 3z²- 6x + 12y – 18z - 6 = 0

x² + y² + z² - 2x + 4y – 6z - 2 = 0